Vous avez des données avec une colonne par variable et vous voulez décrire ces données. La première étape consiste en l’utilisation de statistiques descriptives univariées vous permettant d’obtenir des informations sur chaque variable séparément. Il s’agit ici de statistique sur des échantillons , ils permettent (si l’échantillon est représentatif) d’estimer un paramètre sur la population.
On différencie deux types de variables :
- les variables quantitatives : il s’agit de valeurs numériques, on les appelles aussi continues,
- les variables qualitatives : il s’agit de variables dont le nombre de valeurs possibles est limité. Ces valeurs sont appelées modalités.
Statistiques pour décrire une variable quantitative
La description d’une variable quantitative se base sur les statistiques suivantes : la moyenne, la médiane, la variance, l’écart-type, les quantiles. On peut aller plus loin en regardant l’asymétrie et l’aplatissement.
La moyenne
C’est la statistique de position par excellence. Elle est une somme pondérée. Il s’agit de la somme des valeurs associées à la variable étudiée divisée par le nombre d’individus. Si des poids sont utilisés, il s’agit de la somme des produits poids-valeurs divisé par la somme des poids.
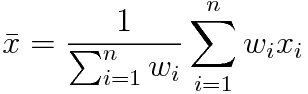
La moyenne est la statistique utilisée en premier dès qu’on a des variables quantitatives. Elle a néanmoins un défaut, elle est très influencée par les valeurs extrêmes de l’échantillon.
-
Calcul d’une moyenne avec R
Les fonctions pour calculer une moyenne et une moyenne pondérée avec R sont :
mean(x) weighted.mean(x,w) -
Calcul d’une moyenne avec Excel
Les fonctions pour calculer une moyenne et une moyenne pondérée avec Excel sont :
=moyenne(A1:A5) =SOMMEPROD(A1:A4;B1:B4)/SOMME(B1:B4)
Liens et références
La médiane
C’est aussi une statistique de position, elle se calcule très simplement et offre une alternative intéressante à la moyenne car elle ne dépend pas des valeurs extrêmes de la distribution.
La médiane est la valeur tel que la moitié des observations de l’échantillon ont des valeurs supérieures et l’autre moitié ont des valeurs inférieures.
On la calcule de la manière suivante :
- Si le nombre d’observations de l’échantillon est impair alors il s’agit de l’observation x[n/2+1], sachant que les x[i] représentent l’observation se trouvant en ième position après tri des observations.
- Si le nombre d’observations de l’échantillon est pair, on prendra la valeur
Elle est toujours représentée sur les box-plot (boîtes à moustaches) et sert pour le calcul de nombreux tests non paramétriques. La médiane est le 0.5-quantile.
-
Calcul de la médiane avec R
La fonction pour calculer une médiane avec R est :
median(x) -
Calcul d’une médiane avec Excel
La fonction pour calculer une médiane avec Excel est :
=MEDIANE(A1:A5)
Liens et références
La variance et l’écart-type
La variance et l’écart-type sont des statistiques de dispersion. Elles permettent de mesurer la dispersion des valeurs des observations par rapport à la moyenne.
La variance se calcule par la somme des carrés des différences entre chaque observation et la moyenne divisé par le nombre d’observations. L’écart-type est égal à la racine carrée de la variance.
On utilise souvent l’écart-type car son ordre de grandeur est similaire à celui des données (alors que la variance est une somme de carrés).
Pourquoi diviser par N ou N-1 pour calculer la variance ?
C’est une question récurrente, lorsqu’on calcule une variance on peut diviser soit par N soit par N-1 la somme des carrés des écarts à la moyenne.
On appelle variance sur l’échantillon, la variance lorsqu’on utilise une estimation de la moyenne et on divise alors par N-1. On dit de cette variance qu’elle est non biaisée.
On appelle variance sur la population lorsqu’on utilise la valeur de la moyenne sur la population et on divise alors par N. C’est le premier cas qui est généralement préféré.
-
Calcul d’une variance et d’un écart-type avec R
La fonction pour calculer une variance avec R est :
La fonction pour calculer l’écart-type avec R est :var(x)sd(x) -
Calcul d’une variance et d’un écart-type avec Excel
La fonction pour calculer une variance avec Excel est :
La fonction pour calculer l’écart-type avec Excel est :=VAR(A1:A5)
=ECARTYPE(A1:A5)
Liens et références
Les quantiles
Les quantiles sont des valeurs auxquelles on associe une probabilité p entre 0 et 1 tels que la proportion d’observations ayant des valeurs plus grandes que le quantile recherché soit égal à p. On note généralement p-quantile.
La médiane est le 0.5-quantile, les quartiles sont les 0.25-quantile et 0.75-quantile, le minimum est le 0-quantile et le maximum est le 1-quantile.
On retrouve différentes définitions des quantiles dans la littérature afin de calculer les valeurs exactes des quantiles. On peut voir ce lien pour une description des méthodes (il y en a 9 décrites).
Les quantiles à 00025 et à 0.075 sont souvent utilisés pour calculé un intervalle de confiance non paramétrique à 95%.
On appelle centiles ou percentiles, les quantiles ramenés sur une échelle entre 0 et 100.
-
Calcul de quantiles avec R
La fonction pour calculer des quantiles avec R est :
Cette fonction va calculer le minimum, les quartiles, la médiane et le maximum.quantile(x, probs = seq(0, 1, 0.25)Dans ce cas,c’est la méthode … qui est utilisée par défaut.
-
Calcul des quantiles avec Excel
La fonction pour calculer des quantiles avec Excel est :
p est la probabilité entre 0 et 1.=CENTILE(A2:A5; p)
Liens et références
- Les quantiles avec R
- Les quantiles avec Excel
- Cette référence rassemble les méthodes utilisées :
Hyndman, R. J. and Fan, Y. (1996) Sample quantiles in statistical packages, American Statistician 50, 361–365.
Statistiques pour décrire une variable qualitative
La description d’une variable qualitative est beaucoup plus sommaire. Une fois les modalités de la variable identifiées, il s’agit d’identifier le mode et d’étudier les proportions associées à chaque modalité.
Il sera souvent plus intéressant de croiser des variables qualitatives afin d’extraire plus d’information.
Le mode
Cette statistique représente la modalité la plus représentée dans la variable.
- Il n’y a pas de fonction standard pour calculer le mode, vous pouvez soit utiliser le package modeest et la fonction mlv :
soit utiliser cette fonction :library(modeest) mlv(x, method = "mfv")
Mode = function(x) { ux = unique(x) ux[which.max(tabulate(match(x, ux)))] -
Calcul du mode avec Excel
La fonction pour calculer un mode avec Excel est :
=MODE(A2:A5)
Liens et références
Les proportions par modalité
Le mode en lui-même n’apporte que peu d’information, il est souvent beaucoup plus intéressant d’observer la proportion de chaque modalité dans l’échantillon. Il s’agit d’une valeur entre 0 et 1 associée à chaque modalité tel que la somme de ces valeurs soit égale à 1. Elles sont généralement données sous forme de tableau.
-
Calcul des proportions avec R
La fonction pour calculer les proportions avec R est :
mais ceci ne donnera que le nombre d’observations associées à chaque modalité. Pour obtenir les pourcentage, on peut utiliser la fonction freq du package questionr :table(x)
library(questionr) freq(x) -
Calcul des proportions avec Excel
Il n’y a pas de formules directes pour calculer les proportions de chaque modalité avec Excel.
Et maintenant ?
Vous connaissez une peu mieux vos données, vous pouvez donc les analyser plus finement en utilisant, par exemple, des méthodes bivariées ou même en les modélisant grâce à d’autres variables.
Suivez nos formations !
Vous voulez maîtriser l’utilisation des méthodes d’analyse de données (analyses statistiques, analyses multivariées, méthodes PLS…) et des principaux logiciels et langages de programmation (R, python, SPSS, XLSTAT…), inscrivez-vous à nos formations !Partager cet article

Comments 5
MERCI BIENNN
Il n’y a pas trop à dire car le cours est simple, très facile de comprendre. Mais ce que je peux suggérer c’est peut-être d’ajouter un peu plus des illustrations comme par exemple sur les box-plots et peut être de mettre un petit commentaire dessous afin de beaucoup facilités d’avantage les débutants sur la compréhension. Merci
tres bon travail.
Intéressant
Merci à vous. Je valide