Méthodes statistiques
La sélection d’une méthode d’analyse de données constitue une étape essentielle dans le processus d’exploration des données. Avec le développement du machine learning et des approches liées au big data, le nombre de techniques statistiques disponibles ne cesse de croître, offrant des possibilités d’analyse toujours plus variées et sophistiquées.
Quelle est votre problématique ?
STAT4DECISION a rassemblé un grand nombre de méthodes d’analyse de données et de méthodes statistiques. Contactez-nous si vous avez besoin de conseils.
Décrire
Un quantile à 0.4 (ou 0.4-quantile) est la valeur de l’observation tel que dans l’échantillon ordonné, 40% des observations ont une valeur plus petite que celle recherchée.
La médiane est le 0.5-quantile. Les quartiles sont les 0.25 et 0.75-quantiles.
On appelles centiles ou percentiles les quantiles avec la valeur du paramètre ramenée en pourcentages.
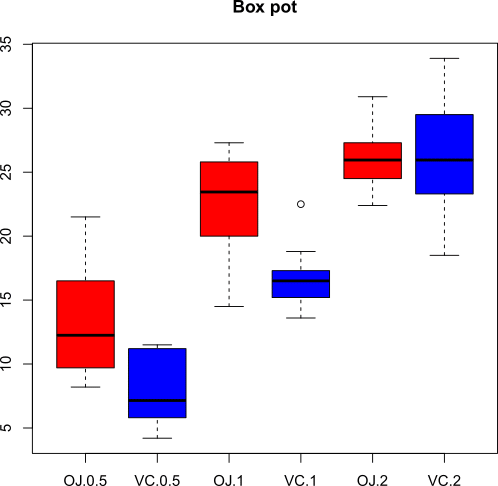
On le représente en général en utilisant un diagramme en bâtons dans lequel les intervalles utilisés sont définis par l’utilisateur. Chaque bâton représente la fréquence des valeurs dans l’intervalle associé.
Modéliser
Il comprend comme cas particulier :
- l’analyse de la variance (ANOVA),
- la régression linéaire,
- l’analyse de la covariance (ANCOVA).
La seule différence entre ces trois approches réside dans la nature des variables explicatives (qualitatives pour l’ANOVA, quantitatives pour la régression linéaire et des deux types pour l’ANCOVA).
Il s’agit d’identifier une relation linéaire entre des variables explicatives indépendantes (X) et une variable à expliquer dépendante (Y). On utilise une estimation par la méthode des moindres carrés pour calculer les paramètres du modèle.
- Un facteur répété est un facteur qui identifie des répétitions d’observations sur les mêmes individus (il peut s’agir de relevés quotidiens de température). On ne peut pas supposer dans ce cas que les observations sont indépendantes ce qui pose un problème pour appliquer le modèle linéaire général. On utilise donc le modèle linéaire mixte qui utilise une matrice de covariance spécifique entre les répétitions couplée à une estimation par le maximum de vraisemblance.
- Un facteur aléatoire est un facteur pour lequel on considère que les modalités présentes dans l’échantillon représentent un échantillon issu d’une population beaucoup plus large (il peut s’agir de parcelles en agronomie, le facteur parcelle contient toutes les parcelles utilisées pour l’expérience en tant que modalités mais on ne peut pas supposer qu’il s’agit de toutes les parcelles possibles). Dans ce cas, on utilisera aussi une matrice de covariance spécifique et une estimation par le maximum de vraisemblance.
Les modèles mixtes sont des modèles avancés permettant de prendre en compte plus de spécificités liées aux données.
- La régression logistique qui suppose une variable dépendante binaire et va permettre de classer des individus dans l’une des deux classes de la variable binaire.
- Le modèle logit multinomial qui suppose une variable dépendante à expliquer qualitative avec plus de deux modalités.
- Le modèle logit ordinal qui suppose une variable dépendante à expliquer ordinale, c’est-à-dire qu’elle se compose d’un nombre limité de modalités qui possèdent une relation d’ordre.
- Le modèle logit conditionnel qui est moins connu que les précédents et qui suppose une variable dépendante qualitative non ordonnée.
Ce modèle de régression va permettre d’expliquer le choix d’une modalité en utilisant les informations liées à toutes les modalités de la variable dépendante. Par exemple, sur le choix d’un mode de transport domicile-travail, on possède des informations sur les 2 variables explicatives qui expliquent le choix (temps de parcours et confort) pour chaque type de transport (transport en commun, vélo, marche à pied, automobile). Chaque individu a choisi un seul moyen de transport mais on veut utiliser toutes les informations sur les différents parcours de l’individu. On aura donc pour chaque individu 4 observations représentant chacune un moyen de transport et à chaque fois deux variables exlicatives. Finalement la variable dépendante sera une variable binaire qui vaudra 1 pour le transport sélectionné et 0 pour les autres. On utilise ainsi plus d’informations que dans un modèle logit classique et on aura donc un résultat plus riche. Ce modèle est par exemple utilisé en analyse conjointe.
Les modèles logistiques offrent de nombreuses interprétations et sont précieux pour l’analyse statistique de variables qualitatives.
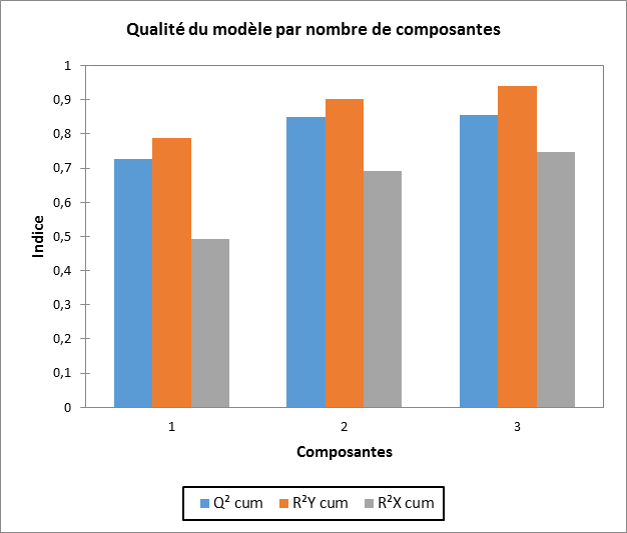
Le principe de cette méthode est simple :
- On effectue une analyse en composantes principales sur les variables explicatives.
- On applique une régression linéaire entre les composantes et la variable dépendante à expliquer.
Le choix du nombre de composantes à conserver doit se faire par l’utilisateur et la construction des composantes principales se fait sans prendre en compte la variable dépendante. Ces deux inconvénients ont fait que l’on préfère souvent utiliser la régression PLS pour ce type de problématique.
Suivez notre prochaine formation sur la régression PLS pour en savoir plus.
- Le cas de multicolinéarité entre les variables indépendantes.
- Le cas d’un tableau avec plus de colonnes que de lignes.
- La présence de données manquantes.
- Le traitement d’un bloc de variables dépendantes (Y est alors une matrice).
Le fonctionnement de l’algorithme est simple :
- On construit des composantes orthogonales à partir des X.
- On construit des composantes à partir des Y.
- On répète des étapes d’ajustement des composantes afin que les composantes de X expliquent le mieux possible les composantes de Y.
A convergence de l’algorithme, on obtient des paramètres du modèle ainsi que des indices de l’importance de chaque variable explicative appelés VIP. L’interprétation de ce type de modèle se fait aussi bien en terme de relation qu’en terme de projection dans les espaces définis par les composantes.
Il existe aussi une variante de cette méthode pour faire de l’analyse discriminante.
Suivez notre prochaine formation sur la régression PLS pour en savoir beaucoup plus.
Analyser
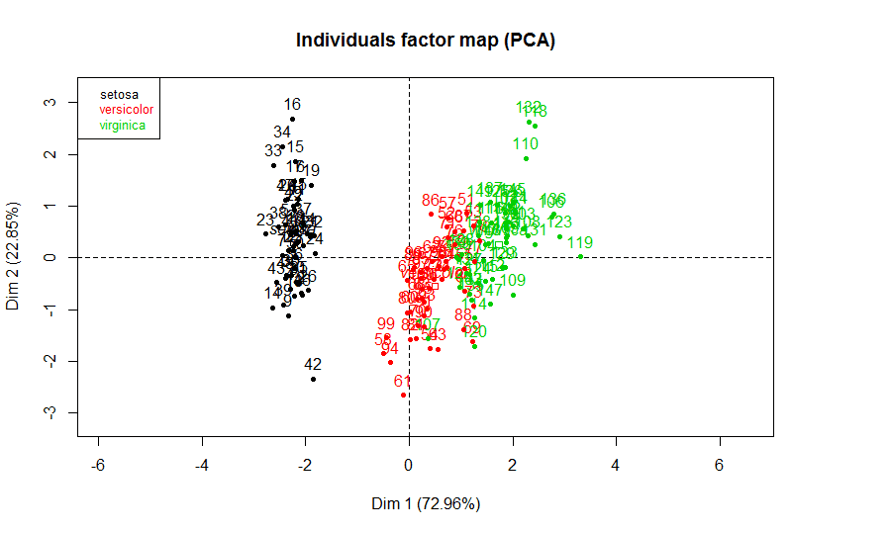
- L’analyse en composantes principales
- L’analyse discriminante
- La classification k-means
- La classification hierarchique
- Les cartes de Kohonen
- L’analyse factorielle multiple (AFM)
- Les analyses de tableaux multiples
- L’ACP mixte
- La méthode Statis
- L'analyse factorielle des correspondances
Tester
- La comparaison de moyennes
- La comparaison de variances
- La comparaison de distribution
- Le test du chi² sur un tableau de contingence
- Les tests non paramétriques de comparaison de 2 échantillons (Mann-Whitney, Wilcoxon)
- Les tests non paramétriques de comparaisons de k échantillons (Kruskall-Wallis, Friedman)
- Les tests non paramétriques de comparaisons de 2 distributions (Kolmogorov-Smirnov)
- Le test de Mantel
- Les tests de corrélations
- Les tests de normalité (Shapiro-Wilk, Jacque-Bera…)